La geometría fractal obedece a una matemática dinámica, del movimiento, del constante fluir..E desarrollo científico del siglo XX pasará a la historia, en la memoria del hombre, por solo tres cosas: la teoría de la relatividad, la mecánica cuántica y la teoría del caos, considerada como la tercera gran revolución científica de este siglo afirman algunos científicosPor ejemplo, la molécula de agua es simple, pero si se congela y se aúna con otras moléculas da origen a las complejas formas de los cristales de nieve. Y ningún cristal es exactamente igual a otro..Ahora sabemos que la Naturaleza se comporta de manera no lineal; hasta hace muy poco no teníamos la posibilidad de un método matemático para estudiar este hecho. Nuestra matemática era lineal, estática. La geometría fractal obedece a una matemática dinámica, del movimiento,La concienciación científica del caos comenzó con los experimentos de Edward Lorenz, en la década de los 60, sobre las variaciones climáticas de la Tierra. Así descubrió el llamado “fenómeno de la mariposa”,Sin embargo, ahora ya sabemos que existe también un superorden dentro del caos, y el aparente caos y casualidad en la vida y la historia obedece a causas y leyes de un nivel superior, dinámico y no lineal.Fue, sin embargo, el físico americano Mitchel Feigenbaum, un romántico que busca su inspiración en Goethe y en Gustav Mahler, quien hizo el gran descubrimiento: la que se ha dado en llamar ley de la universalidad. A mediados de la década de los 70 descubrió el modo concreto en que una conducta regular en un sistema pasa a convertirse en conducta caótica. Observó una clase de traspaso del orden al caos que ocurría en un modelo matemático concreto, y se preguntó si ese mismo traspaso, con los mismos ritmos de cambio, sucedería también en otros modelos. Así, vio que de diferentes ecuaciones matemáticas, de las cuales nadie esperaría que salieran los mismos números, sin embargo salían. El número universal de Feigenbaum es un nuevo número trascendental (como el número áureo, o el número e de los logaritmos neperianos), que permite comprender el caos. Su valor es 4,6692016090, con infinitos decimales más. La universalidad expresa una ley natural de los sistemas en su paso del orden al caos; es válida cualitativa y cuantitativamente, no solo para las formas naturales, sino también para los números exactos. El caos y el azar son la expresión de una ley matemática desconocida hasta ahora, de un superorden de carácter universal, válido para cualquier ser o sistema en comportamiento dinámico. La universalidad significa que sistemas diferentes se comportan del mismo modo, o dicho de otra manera, es el principio hermético de “Como es arriba es abajo, como es abajo es arriba”.
Los sistemas dinámicos caóticos no respondían, sin embargo, a ningún modelo geométrico conocido capaz de describirlos. Se necesitaba una nueva geometría capaz de explicarnos por qué la conducta caótica de la Naturaleza, sus formas informales y dinámicas, nos parecen hermosas y estéticas; explicarnos la estética natural, con sus leyes y causas, de los esquemas caóticos de las nubes, de las montañas, de los relámpagos, de los ríos, de las ramificaciones arborescentes, que no parecían obedecer a ningún orden establecido, a ningún modelo geométrico “lógico” y no casual.
La geometría fractal, desarrollada por el matemático americano Benoit Mandelbrot en los años 70, vino a cubrir ese hueco. El contenido de esta nueva geometría son los llamados objetos fractales, cuya característica principal es la autosemejanza; es decir, que cada una de sus partes, en diferentes escalas de magnitud, es semejante al conjunto total. El objeto se repite, se “reproduce” a sí mismo en sus partes, en cualquier escala en que sea considerado. Los objetos fractales son así seres vivos, con capacidad de autorreproducción en lo infinitamente grande y en lo infinitamente pequeño.
Los sistemas dinámicos caóticos no respondían, sin embargo, a ningún modelo geométrico conocido capaz de describirlos. Se necesitaba una nueva geometría capaz de explicarnos por qué la conducta caótica de la Naturaleza, sus formas informales y dinámicas, nos parecen hermosas y estéticas; explicarnos la estética natural, con sus leyes y causas, de los esquemas caóticos de las nubes, de las montañas, de los relámpagos, de los ríos, de las ramificaciones arborescentes, que no parecían obedecer a ningún orden establecido, a ningún modelo geométrico “lógico” y no casual.
La geometría fractal, desarrollada por el matemático americano Benoit Mandelbrot en los años 70, vino a cubrir ese hueco. El contenido de esta nueva geometría son los llamados objetos fractales, cuya característica principal es la autosemejanza; es decir, que cada una de sus partes, en diferentes escalas de magnitud, es semejante al conjunto total. El objeto se repite, se “reproduce” a sí mismo en sus partes, en cualquier escala en que sea considerado. Los objetos fractales son así seres vivos, con capacidad de autorreproducción en lo infinitamente grande y en lo infinitamente pequeño.
Mandelbrot
El Mandelbulb es un análogo tridimensional de la conjunto de Mandelbrot , construido por Daniel White y Paul Nylander usandocoordenadas esféricas . [ 1 ]
A canónica conjunto de Mandelbrot 3-dimensional no existe, ya que no hay análogo 3-dimensional del espacio de 2 dimensiones de los números complejos. Es posible construir conjuntos de Mandelbrot en 4 dimensiones utilizando cuaterniones . Sin embargo, este conjunto no presenta detalle en todas las escalas, como el conjunto de Mandelbrot 2D hace.
Fórmula Blanca y de Nylander para la " n º poder "del vector 3D 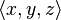 es
es
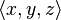 es
es
donde  ,
,  y
y  .
.
 ,
,  y
y  .
.
Ellos usan la iteración  , donde
, donde 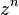 se define como anteriormente y
se define como anteriormente y  es una adición vectorial. [ 2 ] Para n > 3, el resultado es una estructura 3-dimensional de bulbo como con fractal detalle de la superficie y un número de "lóbulos" controlados por elparámetro n . Muchos de sus representaciones gráficas utilizan n = 8. Las ecuaciones pueden simplificarse en polinomios racionales para cada n impar, por lo que se ha especulado por algunos [ ¿quién? ] que las potencias impares son más elegante . Por ejemplo n = 3 se simplifica a:
es una adición vectorial. [ 2 ] Para n > 3, el resultado es una estructura 3-dimensional de bulbo como con fractal detalle de la superficie y un número de "lóbulos" controlados por elparámetro n . Muchos de sus representaciones gráficas utilizan n = 8. Las ecuaciones pueden simplificarse en polinomios racionales para cada n impar, por lo que se ha especulado por algunos [ ¿quién? ] que las potencias impares son más elegante . Por ejemplo n = 3 se simplifica a:
 , donde
, donde 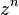 se define como anteriormente y
se define como anteriormente y  es una adición vectorial. [ 2 ] Para n > 3, el resultado es una estructura 3-dimensional de bulbo como con fractal detalle de la superficie y un número de "lóbulos" controlados por elparámetro n . Muchos de sus representaciones gráficas utilizan n = 8. Las ecuaciones pueden simplificarse en polinomios racionales para cada n impar, por lo que se ha especulado por algunos [ ¿quién? ] que las potencias impares son más elegante . Por ejemplo n = 3 se simplifica a:
es una adición vectorial. [ 2 ] Para n > 3, el resultado es una estructura 3-dimensional de bulbo como con fractal detalle de la superficie y un número de "lóbulos" controlados por elparámetro n . Muchos de sus representaciones gráficas utilizan n = 8. Las ecuaciones pueden simplificarse en polinomios racionales para cada n impar, por lo que se ha especulado por algunos [ ¿quién? ] que las potencias impares son más elegante . Por ejemplo n = 3 se simplifica a:
enlaces











.jpg)